TP1 - Introduction à la programmation dynamique
- Comprendre le concept de la programmation dynamique ;
- Mettre en place une solution dynamique ;
- Évaluer la complexité algorithmique.
Les parties 1 et 2 se font sur papier.
La partie 3 se programme sur python.
La Communauté des Lapins
Dans la forêt Domaniale d'Ormont-Robache, un cuniculteur (éleveur de lapins) possède une espèce rare de lapin, qui, lorsqu'ils se reproduisent, donnent naissance uniquement à un nouveau couple de bébés lapins.
Ce couple de bébés lapins est alors capable de se reproduire à partir du deuxième mois, en donnant naissance à son tour à un couple de lapins.
On souhaite compter combien de couple de lapins obtiendra le cuniculteur après un certain nombre de mois.
On obtient le graphique suivant :
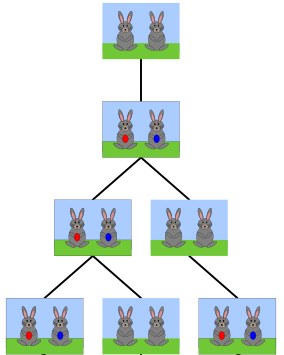
- Mois "0" : le cuniculteur n'a pas de lapins. Il y a
0couple. - Mois "1" : le cuniculteur adopte un couple de bébés lapins ne pouvant se reproduire. Il y a
1couple. - Mois "2" : le couple de lapins grandit et peut se reproduire. Il y a
1couple. - Mois "3" : le couple de lapins se reproduit, et
donne naissance à un couple de bébés lapins. Il y a
2couples. - Mois "4" : le couple de lapins se reproduit, et donne naissance à un couple de bébés lapins. Le couple de lapins du mois 2 grandit et peut se reproduire. Il y a
3couples.
- Dessiner l'arbre pour le mois 4. Combien de couple de lapins possède le cuniculteur ?
- Déterminer le lien entre le nombre de couples de lapin du mois 4 avec le nombre de couples des mois précédents.
- En se basant sur l'arbre (sans le compléter) et le lien trouvé précédemment, trouver le nombre de couples existants au mois 8.
Les Deux Façons de programmer Fibonacci
On rappelle que la suite Fibonacci permet de calculer le terme n de la suite suivant la somme entre le terme n-1 et le terme n-2 de la suite. On obtient ainsi :
- À l'initialisation : F0 = 0
- À la première étape : F1 = 1
- À l'étape 2 : F2 = F1 + F0 = 1 + 0 = 1
- À l'étape n : Fn = Fn-2 + Fn-1
On peut donc modéliser les appels sous la forme d'un arbre.
- Dessiner l'arbre correspondant à l'appel de F4.
- Calculer la valeur de F4.
- Combien de fois apparaît F3 ? F2 ?
- Écrire la fonction récursive
fibonacciRec(n)qui calcule récursivement et retourne le n-ième terme de la suite de Fibonacci.
On se retrouve, avec la méthode récursive, à recalculer des termes qui ont déjà été calculés.
Ce n’est ni optimal en terme de temps, ni en terme d’espace.
Il faut réfléchir à une solution permettant de calculer un terme de la suite de Fibonacci sans avoir à recalculer à chaque fois les mêmes termes.
Le Retour de Fibonacci
Pour éviter d’avoir à recalculer des termes, on va stocker chaque terme calculé dans une liste.
L’indice de cette liste sera le terme de la suite.
suite = [0,1] #0 et 1 étant respectivement les valeurs du terme 0 et 1
#Le 2ème élément est calculé par la somme de l'élément 1 avec l'élément 0
suite.append(suite[1] + suite[0])
- Écrire la fonction itérative
fibonacciDynamique(n)qui prend un entier n en paramètre, et retourne le n-ième terme calculé avec la suite de Fibonacci.
Petit coup de pouce pour les gros problèmes
On souhaite transformer cette fonction en une fonction récursive.
- Écrire la fonction récursive
fibonacciDynamiqueRec(n,l)qui prend un entier n ainsi qu’une liste en paramètres, et retourne le n-ième terme calculé avec la suite de Fibonacci.
On souhaite comparer les temps d’exécution des fonctions en utilisant la bibliothèque time.
Pour tester le temps d'exécution d'un programme, on peut utiliser la structure suivante :
import time
t1 = time.time()
#exécution du programme
t2 = time.time()
print("temps écoulé : ",t2-t1)
t1 et t2 sont des variables contenant le temps au moment où sont déclarées les variables. Ainsi le temps d'exécution d'un programme correspond à la différence de t2 par t1.
- Calculer le temps d’exécution de la suite de Fibonacci en récursif et en dynamique avec les données du tableau ci-dessous, et le compléter sur excel.
Élément 10 20 30 31 33 35 37 40 Récursif Dynamique Itératif Dynamique Récursif - Tracer la courbe représentant le temps d’exécution de ces 3 fonctions.