La programmation dynamique

Introduction

La programmation dynamique est une méthode permettant de résoudre des problèmes d'optimisation, inventée par Richard Bellman dans les années 1950.

Son fonctionnement consiste à :

• Diviser le problème initial en sous-problèmes ;
• Résoudre individuellement chaque sous-problème ;
• Stocker les résultats obtenus lors de la résolution des sous-problèmes, pour les réutiliser.

Exemple d'application avec Fibonacci

La suite de Fibonacci, dans sa version récursive, n'est pas optimale. On se rend vite compte qu'un peu avant le calcul du 30ème terme, le programme met plusieurs minutes à obtenir un résultat.

On a le programme récursif suivant :

def fibonacci(n):
    if n == 0 :
        return 0
    elif n == 1 :
        return 1
    else :
        return fibonacci(n-1) + fibonacci(n-2)

Si on calcule le 6ème terme de cette suite, on peut obtenir l'arbre suivant :

De nombreuses branches

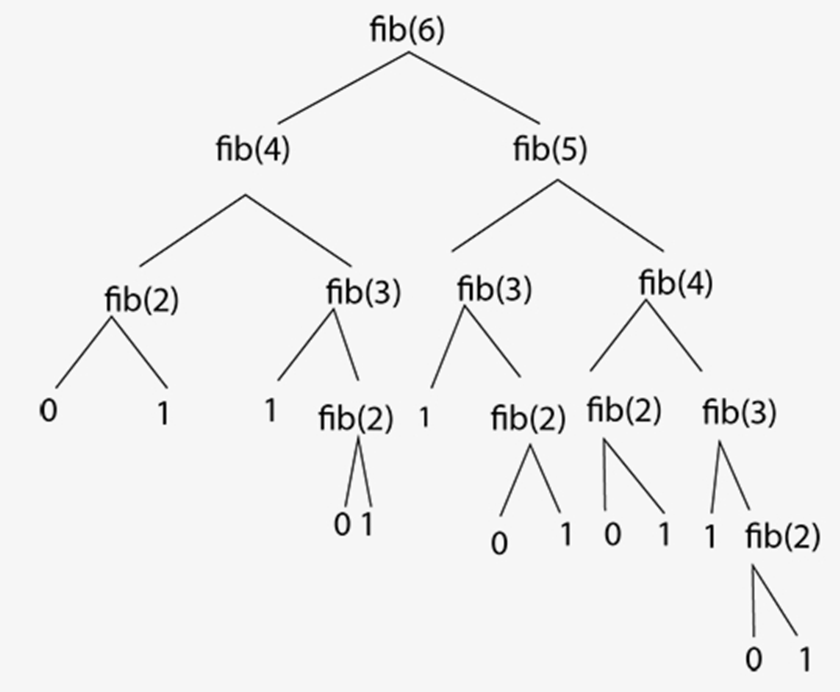
On peut remarquer qu'il existe plusieurs fois les mêmes appels de fonction, dans plusieurs branches de l'arbre.

En calculant le temps d'exécution de cette fonction avec plusieurs termes, on peut obtenir cette courbe :

Complexité

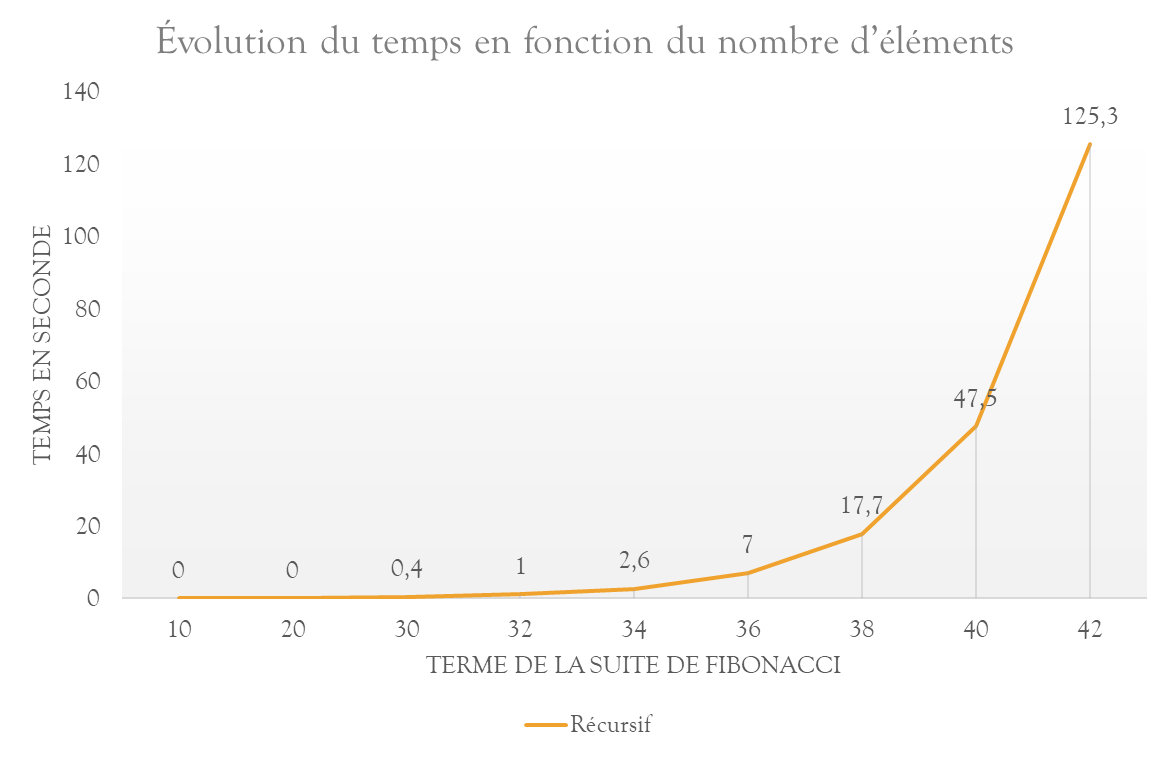
Dans cet exemple, la version récursive de la suite de fibonacci offre une complexité temporelle et spatiale exponentielle.

Mémoïsation

Mémoïser

Le concept même de la programmation dynamique consiste à stocker, sauvegarder, mémoïser les solutions obtenues à chaque sous-problème donné, pour les réutiliser dans la solution finale du problème initial.

La mémoïsation se fait dans une structure de données appropriée (liste, matrice, dictionnaire, objet ...).

Dans le cas de la suite de Fibonacci, la mémoïsation s'utilise avec une liste, où chaque indice de la liste correspond à un terme de la suite, et chaque élément de liste contient la valeur calculée de la suite, au terme donné.

Exemple

On souhaite calculer le 6ème terme de la suite. Initialement avec la version récursive, on aurait, en terme de calcul, l'arbre donné plus haut.
Avec la mémoïsation, l'arbre ressemblerait à ceci :

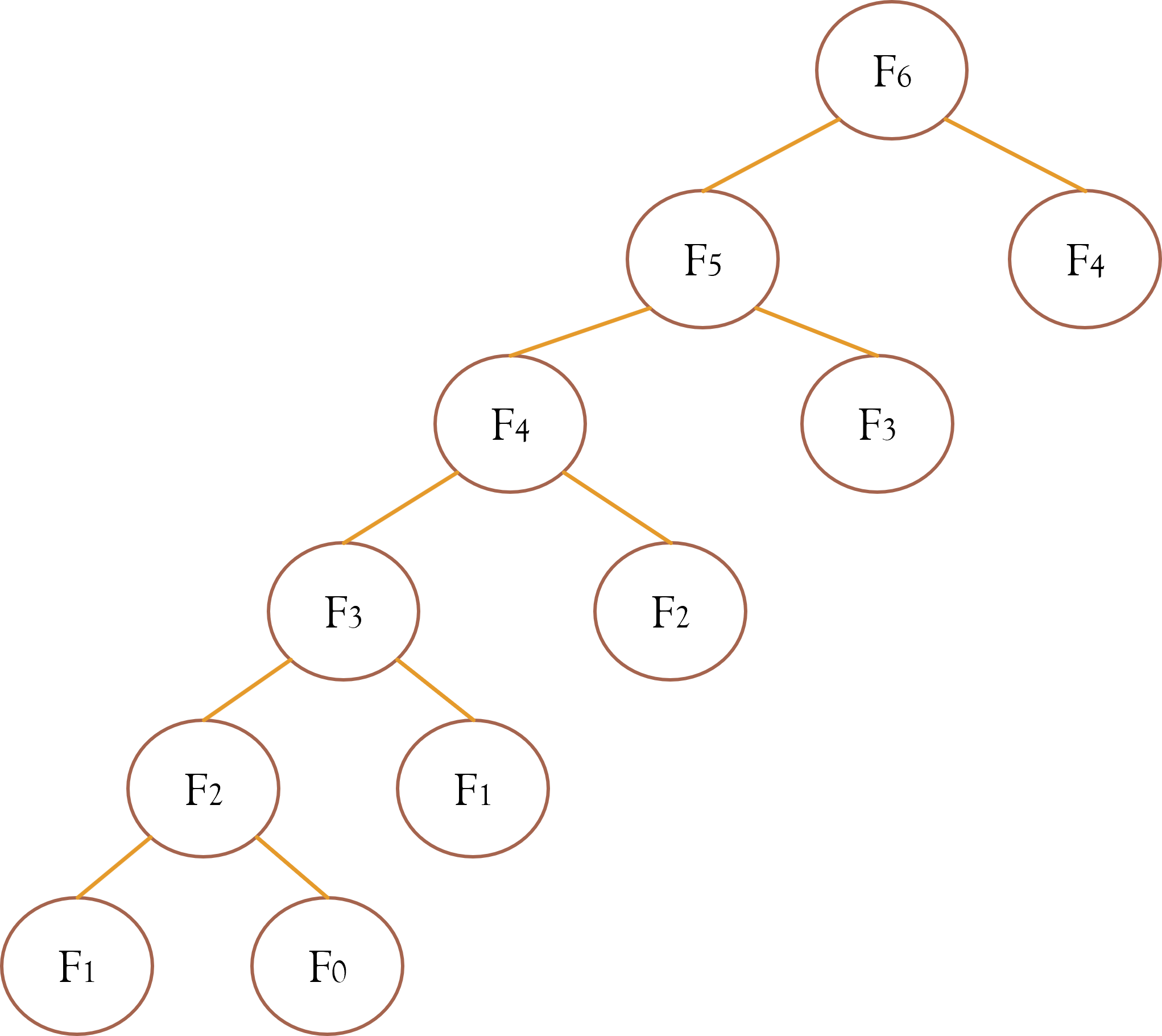
Où chaque noeud ne correspond qu'à un accès dans la liste à la valeur du terme correspondant à l'indice.

Avec la liste, on aurait à l'initialisation :

Indice (terme)	0	1
Valeur	0	1

Puis, pour chaque terme à calculer en plus, on ajouterait dans cette liste un nouvel élément, qui aurait pour valeur la somme des 2 éléments précédents :

• Terme 2 = Terme 1 + Terme 0

  Indice (terme)	0	1	2
  Valeur	0	1	1

• Terme 3 = Terme 2 + Terme 1

  Indice (terme)	0	1	2	3
  Valeur	0	1	1	2

• Terme 4 = Terme 3 + Terme 2

  Indice (terme)	0	1	2	3	4
  Valeur	0	1	1	2	3

• Terme 5 = Terme 4 + Terme 3

  Indice (terme)	0	1	2	3	4	5
  Valeur	0	1	1	2	3	5

• Terme 6 = Terme 5 + Terme 4

  Indice (terme)	0	1	2	3	4	5	6
  Valeur	0	1	1	2	3	5	8