Les protocole de routage
En réseau, les protocoles de routage assurent l'acheminement des paquets entre les différents routeurs. En NSI, nous en étudions 2 spécifiques :
- Le protocole RIP ;
- Le protocole OSPF.
Avant d'étudier les protocoles, il est important de schématiser des réseaux de façon simple, à l'aide de graphes.
Dessin, schéma, représentant un ensemble de sommets, reliés entre eux par un ensemble d’arêtes, modélisant des situations.
Représenté par un cercle avec une valeur dedans, il représente un élément d'une situation que l’on souhaite modéliser.
Ici, un sommet représente un routeur (on ne compte pas les ordinateurs).
Liaison entre 2 sommets, schématise le lien qu'il peut y avoir entre des sommets, dans la situation à modéliser.
Ici, une arête entre 2 sommets représente la connexion entre 2 routeurs.
Prenons le réseau suivant :
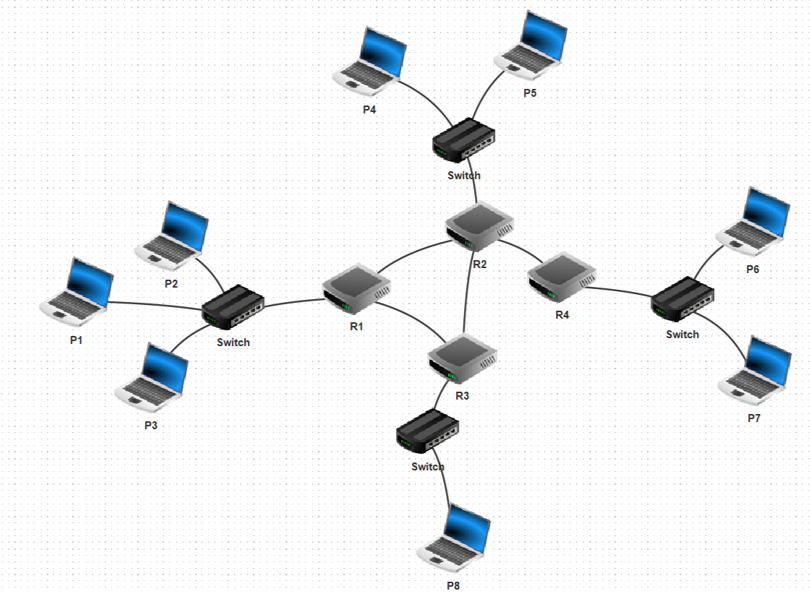
Pour le transformer en graphe, on va dans un premier temps mettre en avant les routeurs présents :
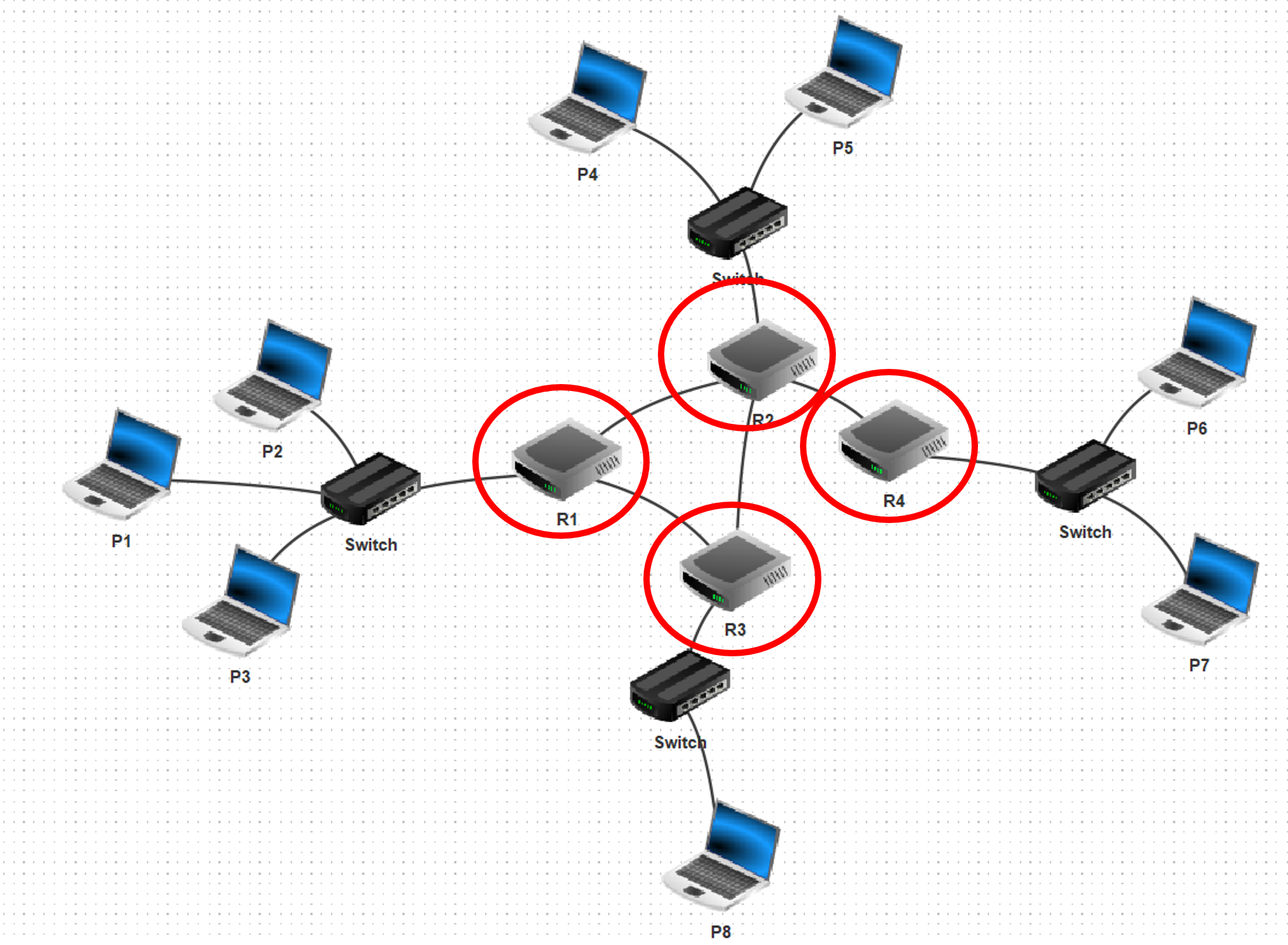
Puis, on peut dessiner des sommets, dans lesquels on marque le numéro/nom du routeur, en les reliant comme le proposait le montage initial :
Les graphes (petit spoiler) utilisent différents algorithmes permettant d'effectuer des recherches de chemins (le chemin le plus court, le chemin le moins coûteux, ...).
De ce fait, acheminer des données dans un réseau revient à chercher des chemins entre des routeurs, qui soient le plus court, voire le moins coûteux, et donc la modélisation sous la forme d'un graphe simplifie le travail.
Le protocole RIP
Le protocole RIP (Routing Information Protocol) reprend l'algorithme de Bellman-Ford, et consiste à chercher le chemin le plus court en déterminant le nombre de sauts à effectuer entre un routeur de départ et un routeur d'arrivé.
On souhaite aller du sommet 1 au sommet 4. Il existe 2 chemins possibles :
- 1 - 2 - 4 : on effectue
2 sauts; - 1 - 3 - 2 - 4 : on effectue
3 sauts.
Le protocole RIP va prendre le chemin où l'on effectue le moins de sauts possibles; on prendra donc le chemin 1 - 2 - 4.
En réseau, chaque routeur va donc avoir une table de sauts, associant pour chaque routeur :
- Un routeur d'arrivée ;
- Le routeur par lequel on doit passer pour aller à celui d'arrivée ;
- Le nombre de sauts nécessaires pour aller au routeur d'arrivée.
Pour l'exemple donné, on aurait :
- Routeur 1
- Routeur 2
- Routeur 3
- Routeur 4
| Destination | Sommet suivant | Saut |
|---|---|---|
| Sommet 1 | Sommet 1 | 1 |
| Sommet 2 | Sommet 2 | 1 |
| Sommet 3 | Sommet 3 | 1 |
| Sommet 4 | Sommet 2 | 2 |
| Destination | Sommet suivant | Saut |
|---|---|---|
| Sommet 1 | Sommet 1 | 1 |
| Sommet 2 | Sommet 2 | 1 |
| Sommet 3 | Sommet 3 | 1 |
| Sommet 4 | Sommet 4 | 1 |
| Destination | Sommet suivant | Saut |
|---|---|---|
| Sommet 1 | Sommet 1 | 1 |
| Sommet 2 | Sommet 2 | 1 |
| Sommet 3 | Sommet 3 | 1 |
| Sommet 4 | Sommet 2 | 2 |
| Destination | Sommet suivant | Saut |
|---|---|---|
| Sommet 1 | Sommet 2 | 2 |
| Sommet 2 | Sommet 2 | 1 |
| Sommet 3 | Sommet 2 | 2 |
| Sommet 4 | Sommet 4 | 1 |
À partir du graphe suivant :
Écrire les tables de saut pour chaque routeur.
Le protocole OSPF
Le protocole OSPF (Open Shortest Path First) reprend l'algorithme de Dijkstra, et consiste à chercher le chemin le moins coûteux, c'est-à-dire celui dont la somme des arêtes entre le routeur de départ et celui d'arrivé est la plus faible.
Les graphes sont valués, leurs arêtes possèdent un poids représenté ici par le débit de transfert entre un routeur A et un routeur B.
Concrètement, une valeur sera associée à chaque arête, correspondant à la vitesse de transfert entre 2 routeurs.
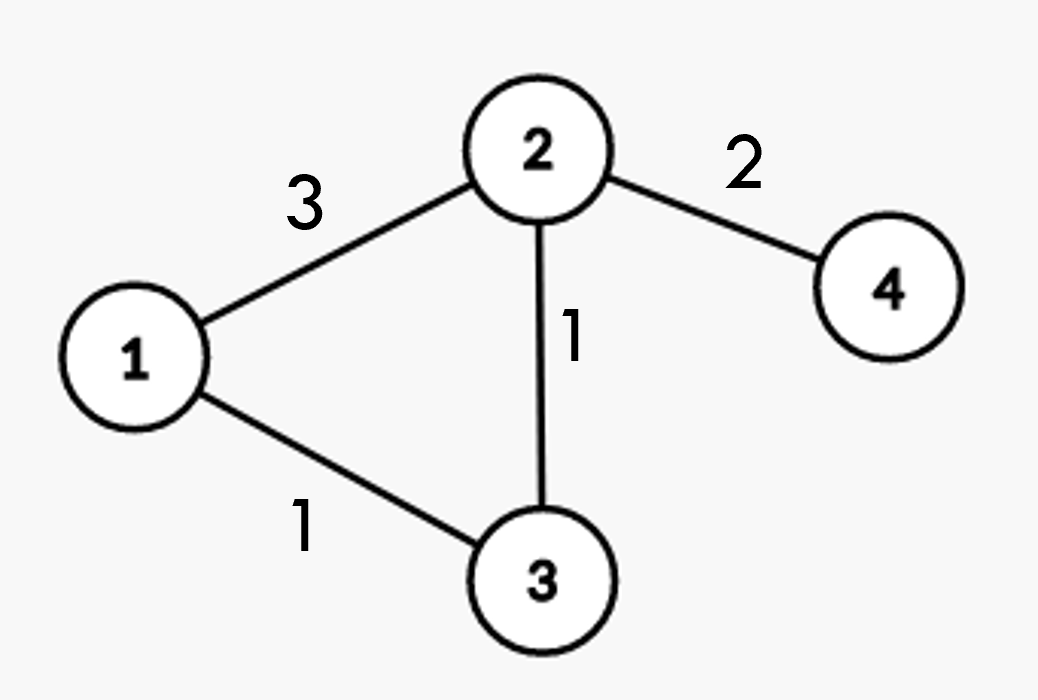
On souhaite aller du sommet 1 au sommet 4. Il existe 2 chemins possibles :
- 1 - 2 - 4 : la somme des arêtes de ce chemin est de
5; - 1 - 3 - 2 - 4 : la somme des arêtes de ce chemin est de
4.
Le protocole OSPF va prendre le chemin où l'on prend le moins de temps de transfert possibles; on prendra donc le chemin 1 - 3 - 2 - 4.
La méthode consiste à utiliser un tableau des « coûts » pour aller d’un sommet à un autre, que l’on va mettre à jour à chaque itération, jusqu’à arriver au sommet de destination.
On initialise ce tableau en mettant la valeur « ∞ » à tous les sommets, sauf celui de départ, que l’on met à 0.
Pour chaque itération, il faut :
- Mettre à jour la valeur des
sommets voisinsdu sommet de départ, en leur donnant la valeur du sommet de départ additionné au poids de l’arête pour l’atteindre ; - Remplacer la valeur d'un sommet s'il dispose initialement d'une valeur plus grande que celle qui vient d'être trouvée. À contrario, si la valeur calculée est plus grande que celle initialement dans le sommet, on
garde la valeur initiale; - Choisir le sommet avec la plus petite valeur sur la ligne pour finir. Le sommet choisi sera le sommet de départ de la prochaine itération.
Pour l'exemple donné, on aurait :
- Initialisation
- Ité. 1
- Ité. 2
- Ité. 3
| Itération | Sommet 1 | Sommet 2 | Sommet 3 | Sommet 4 | Sommet choisi |
|---|---|---|---|---|---|
| Init | 0 | ∞ | ∞ | ∞ | 1 |
On souhaite aller du sommet 1 au sommet 4, on initialise le tableau, mon sommet choisi est donc le sommet 1 (celui avec la valeur la plus petite).
| Itération | Sommet 1 | Sommet 2 | Sommet 3 | Sommet 4 | Sommet choisi |
|---|---|---|---|---|---|
| Init | 0 | ∞ | ∞ | ∞ | 1 |
| 1 | | 3 | 1 | ∞ | 3 |
Première itération, je pars du sommet 1 (je peux donc griser sa case pour ne plus y retourner), je mets à jour tous ses voisins en additionnant la valeur du sommet 1 (0) avec la valeur des arêtes allant vers les voisins.
Je peux aller vers le sommet 2 disposant d'une arête de 3, donc je mets la somme de 0+3. Je fais la même avec le sommet 3.
Pour finir, je choisis le sommet dont la valeur est la plus petite, donc le sommet 3.
| Itération | Sommet 1 | Sommet 2 | Sommet 3 | Sommet 4 | Sommet choisi |
|---|---|---|---|---|---|
| Init | 0 | ∞ | ∞ | ∞ | 1 |
| 1 | | 3 | 1 | ∞ | 3 |
| 2 | | 2 | | ∞ | 2 |
Je recommence en partant du sommet 3.
Il peut aller vers le sommet 2 avec une arête de 1, je fais la somme de la valeur du sommet 3 avec la valeur de l'arête : 1 + 1.
La valeur 2 obtenue est plus petite que la valeur 3 initialement trouvée pour le sommet 2, ce qui veut dire que le chemin est plus rapide (en terme de débit), je remplace donc la valeur.
Pour finir, je choisis le sommet dont la valeur est la plus petite, donc le sommet 2.
| Itération | Sommet 1 | Sommet 2 | Sommet 3 | Sommet 4 | Sommet choisi |
|---|---|---|---|---|---|
| Init | 0 | ∞ | ∞ | ∞ | 1 |
| 1 | | 3 | 1 | ∞ | 3 |
| 2 | | 2 | | ∞ | 2 |
| 3 | | | | 5 | 4 |
Je remets à jour de la même façon les valeurs.
Je suis arrivé au sommet recherché, je peux donc arrêter l'algorithme, et afficher le chemin à parcourir pour y accéder.
Dans un réseau, le poids des arêtes possèdent pour unité une bande passante, s'exprimant en bits/s.
Il faut d’abord calculer les coûts des arêtes en utilisant la formule suivante :
cout = 108/d
où d représente la bande passante entre 2 routeurs (donc le poids d’une arête).
En général, les coûts les plus faibles sont des débits de l’ordre du Gbits/s (fibre optique par exemple).
La méthode à utiliser pour OSPF : calculer tous les coûts avec la formule et utiliser l’algorithme de Dijkstra.