TP graphes

Graphes orientés

Dans la première partie de ce TP, nous allons commencer par implémenter la classe qui permettra de manipuler des graphes orientés.
Les sommets et les arcs seront gérés grâce à une liste d’adjacence représentée, en python, par un dictionnaire.

Création de la classe GrapheOriente

Dans ce premier exercice, vous allez créer la classe GrapheOriente. Nous viendrons améliorer cette classe avec différentes implémentations de méthodes dans les prochains exercices.

La classe GrapheOriente est définie par un seul attribut que nous nommerons dico_adjacence, représentant la liste d’adjacence du graphe.

Info attribut

Cet attribut est un dictionnaire.

Chaque clé de ce dictionnaire sera un sommet, dont la valeur sera une liste de sommets, représentant les sommets voisins à ce sommet.

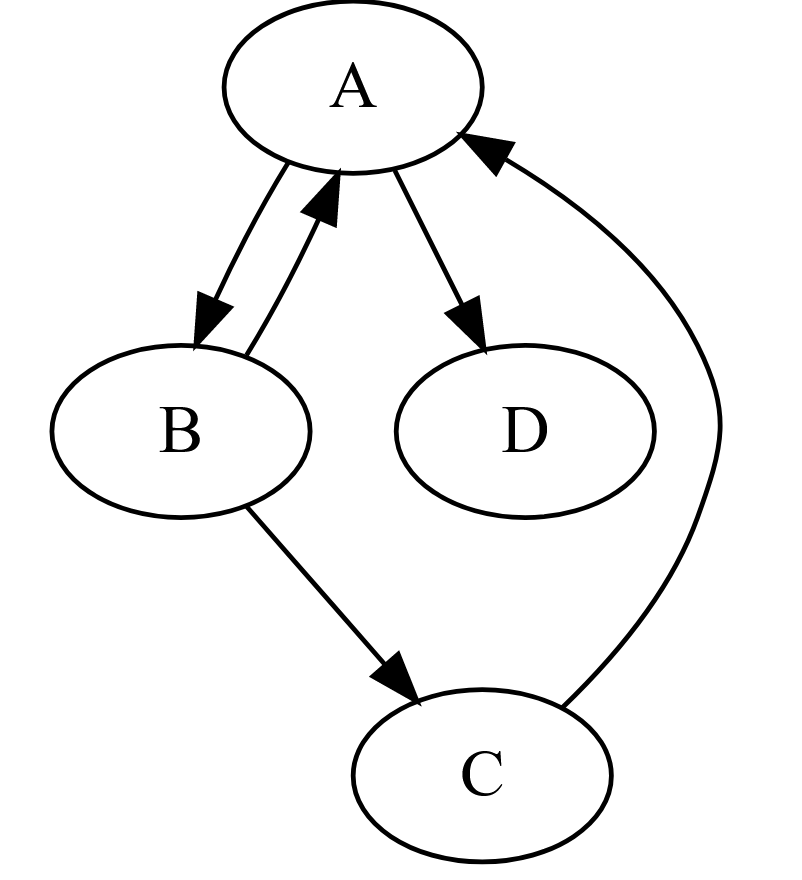
Si on regarde le dictionnaire suivant :

d = {"A":["B", "D"], "B":["A", "C"], "C":["A"], "D":[]}

Cela représente le graphe orienté suivant :

1. Définir la classe GrapheOriente et implémenter son constructeur, qui n’aura pas de paramètres (en dehors de self). Le constructeur devra initialiser l’attribut dico_adjacence avec un dictionnaire vide.

Les sommets

1. Implémenter la méthode ajouter_sommet(self, sommet) qui ajoute, dans l’attribut dico_adjacence de l’objet, une nouvelle clé représentée par le paramètre sommet, en l’associant à une nouvelle liste vide.
   Attention

   Il faut ajouter le sommet seulement si dico_adjacence ne contient pas déjà la clé correspondante (en d’autres termes, seulement si le sommet n’existe pas déjà dans le graphe).

2. Implémenter la méthode sommets(self) qui retourne la liste des sommets du graphe (la liste des clés de dico_adjacence) triée dans l’ordre croissant. On pourra utiliser la fonction sorted de python qui, appliquée sur une liste, retourne la liste triée.
3. Implémenter la méthode contient_sommet(self, sommet) qui retourne True si le graphe contient le sommet passé en paramètre et False sinon.

Tests à effectuer

Recopier le code et exécuter pour tester que tout fonctionne :

test_graphe_oriente = GrapheOriente()
test_graphe_oriente.ajouter_sommet("A")
test_graphe_oriente.ajouter_sommet("B")
test_graphe_oriente.ajouter_sommet("C")
test_graphe_oriente.ajouter_sommet("D")
print(test_graphe_oriente.sommets())
# Affiche ["A", "B", "C", "D"]
print(test_graphe_oriente.contient_sommet("C"))
#Affiche True
print(test_graphe_oriente.contient_sommet("E"))
#Affiche False

Les arcs

1. Implémenter la méthode ajouter_arc(self, sommet_1, sommet_2) qui ajoute sommet_1 et sommet_2 au graphe, puis crée un arc dirigé depuis le premier sommet vers le second. Il faudra ajouter sommet_2 à la liste des voisins de sommet_1 dans l’attribut dico_adjacence de l’objet.
2. Implémenter la méthode arc_existe(self, sommet_1, sommet_2) qui retourne True si l’arc allant de sommet_1 vers sommet_2 existe dans le graphe et False sinon. Il faut vérifier que sommet_2 apparaît bien dans la liste des voisins de sommet_1.

Tests

Afin de faciliter les tests, nous utiliserons une fonction (afficher_graphe(graphe)) qui permettra de visualiser le graphe, provenant du fichier python téléchargeable ici.
ATTENTION il faudra bien avoir respecté le nom de la classe GrapheOriente et de ses attributs.

Placer le fichier afficheur_graphe.py dans le même dossier que le TP en cours.
Importer le module au début du fichier ainsi :

from afficheur_graphe import afficher_graphe
#Tests
mon_graphe = GrapheOriente()
mon_graphe.ajouter_arc("A", "B")
mon_graphe.ajouter_arc("A", "D")
mon_graphe.ajouter_arc("B", "A")
mon_graphe.ajouter_arc("B", "C")
mon_graphe.ajouter_arc("C", "A")
print(mon_graphe.arc_existe("B", "C"))
#Affiche True
print(mon_graphe.arc_existe("C", "B"))
#Affiche False

#Affiche le graphe dans une page web
afficher_graphe(mon_graphe)

Pour la suite des exercices, nous nous baserons sur le graphe orienté suivant, que nous nommerons graphe_oriente_tp :

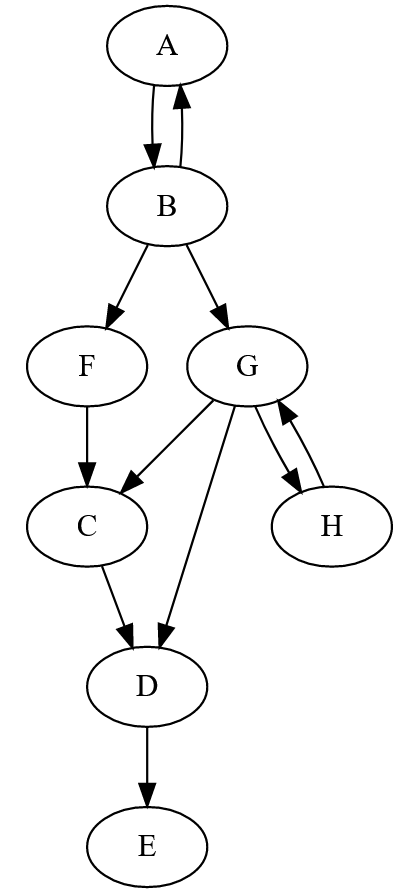
Création d'un GO

1. En utilisant la classe GrapheOriente, créer le graphe ci-dessus, en le stockant dans la variable graphe_oriente_tp.
2. Visualiser le graphe à l'aide de la fonction afficher_graphe.

Voisins d'un sommet

1. Implémenter la méthode voisins(self, sommet) qui retourne la liste des sommets voisins de sommet dans le graphe. La liste devra être triée dans l’ordre croissant (avec sorted).
2. Tester sur graphe_oriente_tp la méthode, avec différents sommets.

Degré d'un sommet

1. Implémenter la méthode degre(self, sommet)qui retourne le degré du sommet passé en paramètre. Pour rappel, pour un graphe orienté, le degré d’un sommet correspondant au nombre d’arcs sortants additionné au nombre d’arcs entrants.
2. Tester sur graphe_oriente_tp la méthode, avec différents sommets.

Graphes non orientés

Dans cette seconde partie du TP, nous allons implémenter la classe qui permettra de manipuler des graphes non orientés.

Rappel vocabulaire

Dans un graphe non orienté, on parle d’arête et non plus d’arc, les liens entre les sommets ne sont plus orientés.
Si un sommet "A" est relié à un sommet "B", le sommet "B" est lui aussi relié au sommet "A"; il y a donc une arête entre "A" et "B" et/ou entre "B" et "A".

La classe GrapheNonOriente est définie de la même manière que la classe GrapheOriente, avec un dictionnaire permettant de gérer la liste des voisins de chaque sommet. Seul l’ajout d’une arête et le calcul du degré d’un sommet diffère. On peut donc dire que GrapheNonOriente est un sous-type de GrapheOriente.

Pour ne pas à avoir à récrire tout le code déjà défini dans GrapheOriente, nous allons utiliser le mécanisme d’héritage.
Nous n’aurons même pas besoin d’écrire de constructeur, car celui-ci est identique à celui de GrapheOriente.

Définir la classe GrapheNonOriente comme suit :

class GrapheNonOriente(GrapheOriente):

Gestion des arêtes

Afin de gérer les arêtes, nous allons redéfinir la méthode ajouter_arc(self, sommet_1, sommet_2) pour pouvoir ajouter un arc.
Lorsqu’une classe "hérite" depuis une autre classe, c’est comme si tout le code de la première classe était copié dans la nouvelle. Le terme "redéfinir" signifie "récrire" le code d’une méthode dans la nouvelle classe pour l’adapter à un comportement voulu. Il suffit de récrire la fonction correspondante.

Le but va être de redéfinir la méthode de telle sorte que lorsqu'on ajoute un arc depuis sommet_1 vers sommet_2, cela crée aussi un arc depuis sommet_2 vers sommet_1. En résumé, sommet_2 est ajouté à la liste des voisins de sommet_1 et inversement. Ainsi, on obtient alors bien une arête.

1. Implémenter la méthode ajouter_arc(self, sommet_1, sommet_2) qui ajoute sommet_1 et sommet_2 au graphe puis crée une arête entre les deux sommets.

Tests à effectuer

Recopier le code et exécuter pour tester que tout fonctionne :

mon_graphe = GrapheNonOriente()
mon_graphe.ajouter_arc("A", "B")
mon_graphe.ajouter_arc("A", "D")
mon_graphe.ajouter_arc("B", "C")
mon_graphe.ajouter_arc("C", "A")
print(mon_graphe.arc_existe("B", "C"))
# Affiche True
print(mon_graphe.arc_existe("C", "B"))
#Affiche True
print(mon_graphe.arc_existe("A", "C"))
#Affiche True
afficher_graphe(mon_graphe)

Pour la suite des exercices de cette section, nous nous baserons sur le graphe non orienté suivant, que nous nommerons graphe_non_oriente_tp :

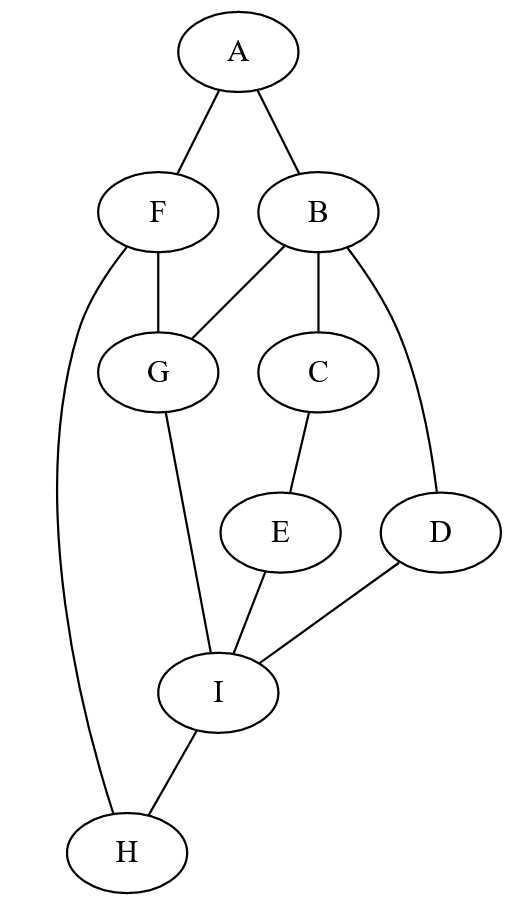
Création d'un graphe non orienté

1. En utilisant la classe GrapheNonOriente, créer le graphe ci-dessus, en le stockant dans la variable graphe_non_oriente_tp.
2. Visualiser le graphe à l'aide de la fonction afficher_graphe.

Degré d’un sommet pour un graphe non orienté

1. Implémenter la méthode degre(self, sommet) qui retourne le degré du sommet passé en paramètre.
2. Tester la méthode sur plusieurs sommets du graphe.

Algorithme sur les graphes

Dans la section suivante, nous allons implémenter les algorithmes dans la classe GrapheOriente. Grâce à l’héritage, la classe GrapheNonOriente aura aussi accès à ces nouvelles méthodes.

Parcours en largeur

Algorithme du parcours

Pour réaliser le parcours en largeur d’un graphe, à partir d’un sommet donné, on utilise une file. La méthode est la suivante :

• On initialise une file puis on y ajoute le sommet de départ ;
• On initialise une structure qui permettra de mémoriser les sommets déjà rencontrés. en python, on utilisera un dictionnaire. On ajoute également le sommet de départ à la structure ;
• Tant que la file n’est pas vide :
  • On retire le sommet courant depuis la file (on le stocke dans une variable) ;
  • On affiche le sommet courant (print) ;
  • Pour chaque voisin du sommet courant, si le voisin n’a pas déjà été rencontré (vérification avec le dictionnaire), on l’ajoute à la file et on l’ajoute aussi comme clé du dictionnaire pour mémoriser qu’on a déjà rencontré ce sommet.

On peut utiliser le dictionnaire en associant le sommet à la valeur True pour indiquer qu’il a déjà été rencontré.
L’utilisation d’un dictionnaire (au lieu d’une liste) est justifiée pour des raisons de complexité temporelle :

sommets_rencontres = {}
#Quand on rencontre un nouveau "sommet" :
sommets_rencontres[sommet] = True
#Pour vérifier si on a déjà rencontré un "sommet"
if sommet in sommets_rencontres:
    ...

1. Importer la classe File (codée lors d’un précédent TP) dans le programme. La classe doit se nommer File et doit se trouver dans un fichier "File.py" :

   from File import File
2. Implémenter la méthode parcours_largeur(self, sommet) qui effectue le parcours en largeur du graphe, à partir du sommet passé en paramètre, en affichant, successivement, les sommets visités.
3. Tester sur graphe_oriente_tp puis graphe_non_oriente_tp à partir du sommet A.

Parcours en profondeur

Algorithme du parcours

Le parcours en profondeur d’un graphe, à partir d’un sommet, a quasiment la même méthode que le parcours en largeur sauf qu’on utilise une pile (et donc, on empile / depile, au lieu d'enfiler / défiler de la file).
Le seul autre changement, se situe au niveau de l’ordre des voisins du sommet courant que l’on traite. Comme on les empile, leur ordre sera inversé. Il faut donc appliquer la fonction reversed sur la liste des voisins parcourue lorsque, dans la boucle, on ajoute les prochains voisins à traiter.

1. Importer la classe Pile (codée lors d’un précédent TP) dans le programme. La classe doit se nommer Pile et doit se trouver dans un fichier "Pile.py" :

   from Pile import Pile
2. Implémenter la méthode parcours_profondeur(self, sommet) qui effectue le parcours en profondeur du graphe, à partir du sommet passé en paramètre, en affichant, successivement, les sommets visités.
3. Tester sur graphe_oriente_tp puis graphe_non_oriente_tp à partir du sommet A.

Trouver un chemin

On souhaite avoir une méthode qui permettrait de trouver un chemin allant d’un sommet à un autre dans le graphe (et ne passant pas deux fois par le même sommet).

À partir du sommet de départ, pour chacun de ses voisins, on regarde si on peut trouver un chemin allant du voisin jusqu’au sommet désiré. Récursivement, le cas d'arrêt serait donc lorsque le sommet de départ est égal au sommet de destination.
La méthode (récursive) est la suivante :

1. On va gérer une liste "chemin" qui sera modifiée et transmise lors des appels récursifs.
2. Au début, on ajoute le sommet "de départ" dans la liste "chemin".
3. Si le sommet de départ et le sommet de destination sont identiques, on retourne la liste cas d'arrêt.
4. Sinon, pour tous les voisins du sommet de départ :
   • Si le voisin n’est pas déjà dans le chemin, on calcule un nouveau chemin (que l’on stocke donc dans une variable) en faisant un appel récursif avec comme paramètre le voisin en question comme sommet de départ, le sommet de destination qui reste inchangé, et enfin, la liste représentant le chemin, et contenant donc le chemin courant, actuellement en cours de construction.
   • Si ce nouveau chemin (liste) calculé n’est pas nul (None), cela signifie qu’on a donc un chemin allant du départ à la destination, on le retourne donc.
5. Quand on sort de la boucle, cela signifie que, à partir du sommet de départ donné en paramètre, on n’a pas pu trouver de chemin allant jusqu’au sommet désiré. On retire donc le sommet de départ de la liste, et on retourne None.

1. Implémenter la méthode trouver_chemin_recursif(self, sommet_depart, sommet_destination, chemin) qui, à partir d’un sommet de départ, un sommet de destination et d’une liste "chemin" (qui est modifiée lors des appels récursifs) retourne une liste représentant le parcours à effectuer (sommet par sommet) pour aller du sommet de départ jusqu’à destination.

On se donne une deuxième fonction trouver_chemin qui permettra d’initialiser le paramètre "chemin" avec une liste vide, et ne pas à avoir à utiliser directement la fonction récursive :

def trouver_chemin(self, sommet_depart, sommet_destination):
    return trouver_chemin_recursif(sommet_depart, sommet_destination, [])

2. Tester la méthode sur graphe_oriente_tp puis graphe_non_oriente_tp :

print(graphe_oriente_tp.trouver_chemin("A", "E"))
#Affiche ['A', 'B', 'F', 'C', 'D', 'E']
print(graphe_oriente_tp.trouver_chemin("G", "E"))
#Affiche ['G', 'C', 'D', 'E']
print(graphe_oriente_tp.trouver_chemin("E", "A") #Ne retourne rien (None)
print(graphe_non_oriente_tp.trouver_chemin("A", "I"))
#Affiche ['A', 'B', 'C', 'E', 'I']
print(graphe_non_oriente_tp.trouver_chemin("D", "G"))
#Affiche ['D', 'B', 'A', 'F', 'G']

Détection de cycles

Dans un graphe, un cycle est un chemin qui commence et termine par le même sommet (on utilise le terme "cycle" pour les graphes non orientés, et "circuit" pour les graphes orientés).

Pour détecter un cycle, dans un graphe, à partir d’un sommet de départ, le but va être de faire une sorte de parcours en profondeur du graphe à partir de ce sommet en mémorisant les sommets rencontrés. Si jamais on rencontre de nouveau un sommet déjà rencontré, on a donc la présence d’un cycle.
La méthode est la suivante :

1. On initialise une pile et on empile le sommet de départ.
2. On initialise un dictionnaire qui stockera les sommets rencontrés (comme dans les parcours en profondeur et en largeur).
3. Tant que la pile n’est pas vide :
   • On dépile un sommet depuis la pile (et on le stocke dans une variable) qui constituera donc le sommet courant.
   • Si le sommet a déjà été rencontré (on regarde avec le dictionnaire), cela veut donc dire qu’un cycle est présent, on retourne True.
   • Sinon, on mémorise, avec le dictionnaire, qu’on a rencontré le sommet.
   • Enfin, pour chaque voisin du sommet courant (dépilé), si le voisin n’a pas déjà été rencontré, on l’empile.
4. Quand on sort de la boucle, cela signifie qu’on a parcouru le graphe depuis le sommet de départ sans détecter de cycle, on retourne donc False.

1. Implémenter la méthode detecte_cycle(self, sommet) qui, à partir d’un sommet, retourne True si un cycle est détecté dans le graphe en partant de ce point et False sinon.
2. Tester la méthode sur graphe_oriente_tp puis graphe_non_oriente_tp.

Cette fonction à elle seule ne permet pas de déterminer si le graphe entier ne contient pas de cycle, notamment si tous les points du graphe ne sont pas reliés, ou, pour un graphe orienté, selon la disposition des arcs. Il faut donc exécuter l’algorithme à partir detous les sommets du graphe pour pouvoir conclure.

3. Implémenter et tester la méthode contient_cycle(self) qui, en vérifiant pour chaque sommet, à l’aide de la méthode detecte_cycle(self, sommet") retourne True si le graphe contient un cycle et False sinon.

Conversion en matrice d'adjacence

Nous aimerions maintenant disposer d’une méthode permettant d’obtenir la matrice d’adjacence à partir du graphe.
En python, la matrice sera représentée par une liste de listes. Chaque liste contenue dans la liste principale représente une ligne de la matrice, et chaque élément des sous-listes représente les colonnes.

Pour un numéro de ligne et un numéro de colonne donnés, la matrice contiendra 1 s'il existe un arc allant du sommet correspondant à la ligne vers la sommet correspondant à la colonne. Si cet arc n’existe pas, la matrice contiendra 0 à cet emplacement. Par exemple, si on prend la matrice suivante :

matrice = [[1,0,1,0],
          [0,1,0,1],
          [1,1,0,1],
          [0,1,1,0]]

On a donc un graphe contenant 4 sommets. Si on prend matrice[0][2], on obtient 1. cela signifie donc qu’il existe un arc entre le sommet 0 et le sommet 2.

1. Implémenter la méthode conversion_vers_matrice(self) qui retourne une matrice correspondant à la matrice d’adjacence du graphe.
2. Tester la méthode sur graphe_oriente_tp puis graphe_non_oriente_tp.